Overview
인공지능이란?
인간의 뇌를 모델링 하는 것
*모델링 : 지능/지식이라는 외부 입력에 의해 이들을 하나의 기능 단위로 여겨 반응을 하는 것 .. 이러한 일련의 과정을 구현하는 것을 모델링
모델링의 방법을 크게 두 가지로 분류 가능
✔️ symbolic : Top down 방식 / 데이터가 모여져 있는 정도에 따라서 black box > gray box > white box로 구분 가능
✔️ connectionist : Bottom up 방식 / 생물학적 뇌는 뉴런으로 구성
🧐 생물학적 뇌
외부의 입력을 받아들여서 처리를 하고 다시 출력물을 내는데, 이러한 출력물이 다른 뉴런의 입력값이 됨
*뉴런의 특징
- 시냅스를 통해서 정보 전달
- 재생하지 않음
- 뉴런은 사멸하면 다시 재생하지 않음
- 어른의 뉴런 = 아이의 뉴런
- 뉴런의 개수보다 연결 방식이 중요
- 재생하지 않는 이유 : 학습 가능성과 연관
- 다수결 동작 원리
- 보통 때는 내부보다 외부가 전압이 높으나, 흥분 시 내부가 외부보다 높음
- 다른 뉴런이 흥분하면 본인도 흥분, 억제하면 본인도 억제
신경 회로망
인공지능이 궁극적으로 하고자 하는 것은 생물학적 시스템의 계산 틀을 구현하는 것
>> 그러나, 실질적으로 컴퓨터로 모방 불가
>> 컴퓨터로 모방은 불가하지만, 정보체계가 어떻게 되어 있는가를 알기 위해 연구 시작
(정보체계는 결국 심리학, 신경 과학, 인지과학, 시스템 이론이 병합 되어서 구현되는 것)
생물학적 신경회로망
어떻게 연결되어 있는가를 알기 위해서 연구 시작
1. 인간의 생체 기능을 연구
2. 동물 생체 실험
3. 학습 능력의 원천을 연구
➡️ 신경회로망의 기능 및 구조를 하드웨어/소프트웨어적으로 실현하여 인공신경회로망 구현
학습
패턴 부류에 따라서 신경망의 연결 가중치를 조정
재생
학습된 가중치와 입력 벡터와의 거리를 계산하여 가장 가까운 클래스로 분류
이를 통해 사람과 같은 학습 능력을 구현할 수 있음 (패턴 분류/인식/최적화/예측)
인공 신경회로망
정의
인간의 두뇌작용을 신경 세포들간의 연결 관계로 모델링 (-> 인간의 학습을 모델링)
특징
- 신경 세포가 신경절로 연결되어 정보를 전달
- 노드 또는 처리 요소를 연결하여 신경 회로망 구현
- 뉴런 1개는 단순 기능이지만, 다중을 연결하여 복잡한 기능을 구현할 수 있는 구조 설계
역사
McCulloch와 Pitts의 주장
- "신경 세포들을 단순 연결한 신경 회로망은 산술 및 논리연산을 수행할 수 있다."
1949년 : Hebb의 법칙
- 최초의 인공 신경회로망의 학습 규칙 제안
- 신경 회로망이 학습을 수행함을 증명
50년, 60년대
- 단층의 인공 세포 신경 회로망
- Rosenblatt, Widrow의 Perceptron : 일기예보/심전도 해석/인공 시각
- ❌ 69년 Minsky에 의해 한계 지적 (Perceptron은 XOR 문제를 해결할 수 없음)
- 신경망 연구 침체 -> symbolism의 부흥
80년대 중반 이후
- symbolism의 한계
- Hopfield : 에너지 개념을 도입한 신경 회로망 주장
- 오류 역전파 학습 알고리즘(= Multi Layer Perceptron) 주장 -> 신경회로망 연구 부흥
뉴런 셀 모델링

✔️ 입력값을 받고 이에 가중치를 곱하여 임계치 설정
✔️ 이를 활성화 함수를 통해서 (아래 3개가 활성화 함수의 종류)
- Sigmoid
- Tanh
- ReLU
✔️ 다른 뉴런의 입력으로 연결
인공 신경회로망 (인공 신경망)의 구조
크게 두 가지의 구조가 존재
- A Single Layer NN
- Single-Output
- Multi-Output
- A Multi Layer NN
*Multi Layer NN의 경우 Hidden Layer가 1단계 이상으로 구성되어 있어서 Layer가 여러 개인 형태를 말함
구조의 단위
- Input unit : 외부로부터 시스템으로 입력을 받아들이는 처리기
- Output unit : 시스템으로부터 출력을 내보내는 처리기
- Hidden unit : 시스템 내에 입출력 값이 모두 있지만 외부에서는 보이지 않는 처리기
- Processing unit (PU)
- Activtion State
- 각 처리기들의 시간이 t일 때, 시스템에서의 상태를 의미
- 시스템이 시간 t에서 나타내는 처리기들의 활성화 패턴
- 연속(아날로그)또는 비연속값(digital, discret)의 값
- Output Function
- 이웃 처리기에 미치는 영향의 정도
- 활성화 함수 적용
- 이 값을 통해서 신호를 전달
- Connectivity (Weight)
- 시스템의 임의의 처리기에 대한 반응 정도
- 각 처리기 사이의 연결 강도를 의미하는 가중치
- 이 값이 클수록 흥분성/억제성 연결을 의미
- Activtion State
Learning Rule
연결 강도를 변화시키는 규칙
연결 가중치 조정 방법
- 지도 학습
- 입력이 주어짐에 따라서 원하는 출력값이 활성화 되도록 (입력과 출력이 모두 주어진 것) 가중치를 조절
- Hopfield 학습 규칙, 델타 규칙, 오류 역전파 학습 규칙
- 비지도 학습
- 목표값 없이 학습 데이터만 입력
- 스스로 연결 가중치들을 학습
- 미리 결정된 출력이 불필요
- 경쟁 학습, ART 모델
인공지능 >> 머신 러닝 >> 딥 러닝
머신 러닝 (= 기계 학습의 종류)
- 지도 학습 (supervised learning)
- 비지도 학습 (unsupervised learning)
- 지도 학습 + 비지도 학습 (semi-supervised learning)
- 강화 학습 (reinforcement learning) : 잘못된 것을 다시 피드백하여 강화
- 진화 학습 (evolutionary learning)
Perceptron
- 1957년 Rosen blatt가 제안한 모델
- 입력 패턴이 두 개의 클래스 중 하나에 속함을 결정할 때 주로 사용되는 모델
Perceptron
- 눈의 망막을 모델화
- 지도 학습 (= 입/출력 존재)
- 이진 & 아날로그 입력 처리
- 전체 출력 뉴런들에 대해서 계산된 출력 값과 목표 값의 차이를 최소화 하는 방식으로 구현
- Widrow-Hoff 규칙 (= 델타 규칙)
- 계산된 출력 값과 목표 값 간의 차이가 없으면 연결 가중치는 변경되지 않음
- 만약 차이가 있다면, 차이를 줄이는 방향으로 가중치를 변경
Perceptron - 단층
출력 값의 층에 따라서 single-output과 multi-output으로 구분할 수 있음
Perceptron - Activation 함수
perceptron의 입출력 과정은 아래와 같음 ⬇️
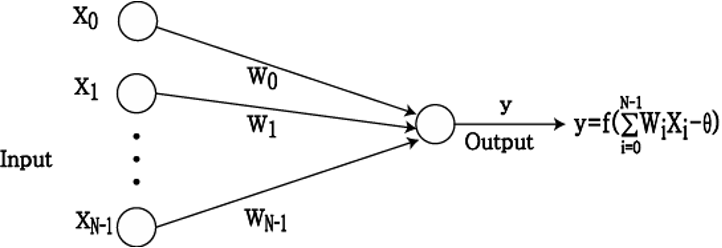
이 때, 출력 값을 내기 위한 활성화 함수 필요
Single Layer NN에서 사용되는 활성화 함수의 형태는 크게 3가지로, 비선형 함수의 형태로 존재
- 계단 함수
- 임계논리 함수
- 시그모이드 함수
Perceptron - Single Perceptron의 학습
- 가중치와 임계치를 초기화
- 새로운 입력 패턴과 목표 출력 패턴을 제시
- 하드리미터 함수를 사용해서 실제 출력값 계산
- 가중치를 계산
- 차이에 따라서 반복 수행 (*여기서 말하는 차이 : 계산된 출력값과 목표 출력값 사이의 차이)
Perceptron - 논리 연산 가능 (AND/OR/NOT 게이트 모두 가능)
AND의 경우 (아래와 같음 ⬇️)
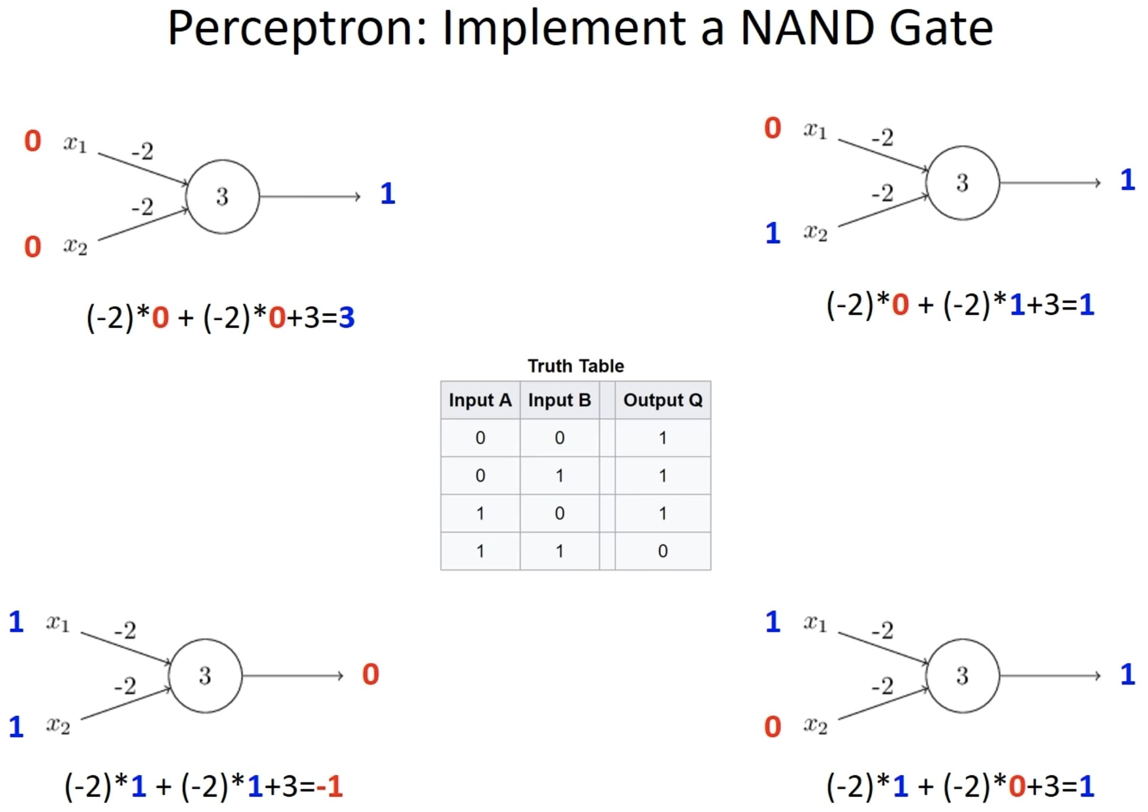
❌ 그러나, 단층 퍼셉트론의 경우 XOR 게이트의 문제는 해결하지 못함 ❌
XOR의 해석
- 만족하는 W0, W1의 값을 구하지 못함
- XOR의 문제 해결 불가
- 이러한 문제를 해결하기 위해서, 2개 또는 3개의 층 구조 필요
- 다층 퍼셉트론 = 3층 퍼셉트론으로 어떤 문제도 해결 가능
🧐 다층 퍼셉트론
- 다층 퍼셉트론은 Delta Rule로는 학습 불가능 (계산된 출력 값과 목표 출력 값의 차이를 비교하는 것)
- 퍼셉트론은 다층 퍼셉트론 및 오류 역전파 알고리즘의 기반 모델이 됨
Perceptron - 한계점
일반적으로 학습이 선형 분리로 가능했지만, XOR 문제에서는 선형 분리가 불가능
>> 만족하는 값을 찾지 못해서 문제 해결 불가
Multi Layer Perceptron
(Single Layer Perceptron의 경우 한계가 존재, 해당 한계를 Multi Layer로 해결 가능)
Multi Layer Perceptron
- 입력층과 출력층 사이에 하나 이상의 은닉층을 갖고 있는 신경 회로망
- 다층 퍼셉트론에 델타 룰 학습 알고리즘을 적용시키는 문제점
- 은닉층의 원하는 목표 출력값을 알 수 없음
- 효과적인 학습 알고리즘이 없어서 60-70년대 사용되지 않음
- >> 이 시기가 NN의 암흑기
- 오류 역전파 (EBP) 알고리즘을 통해서 해결 (-> 오류 알고리즘을 다층 퍼셉트론에 적용)
Multi Layer 구조
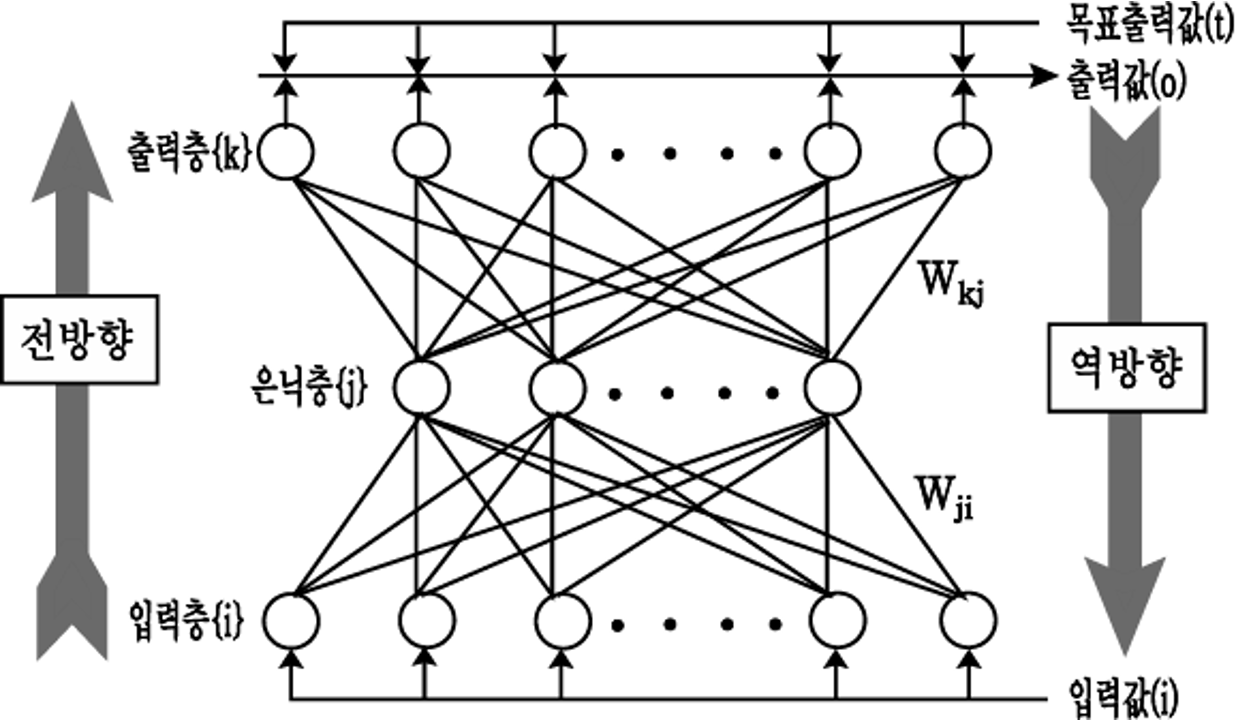
🧐 EBP 알고리즘
- 원하는 목표값(d)과 실제 출력값(o) 사이의 오차 제곱합으로 정의된 비용 함수 E의 값을 경사하강추적법에 의해 최소화하는 방향으로 학습
[더보기] -> 경사하강법
경사하강법
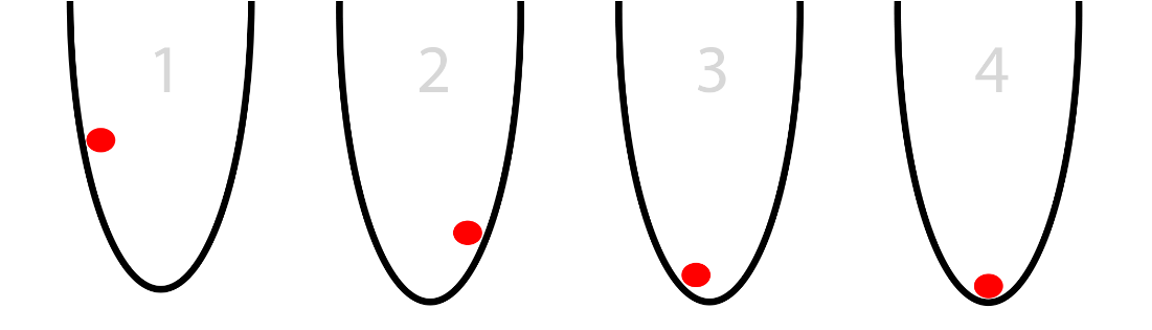
위와 같이 동그란 바구니에 빨간 공이 있다고 가정, 빨간 공은 바구니의 바닥 지점을 찾으려고 함
>> 이 과정을 최적화 과정이라고 함
(공의 위치를 왼쪽에서 오른쪽으로 움직이면서 바구니에서 가장 낮은 지점을 찾으려 최적화)
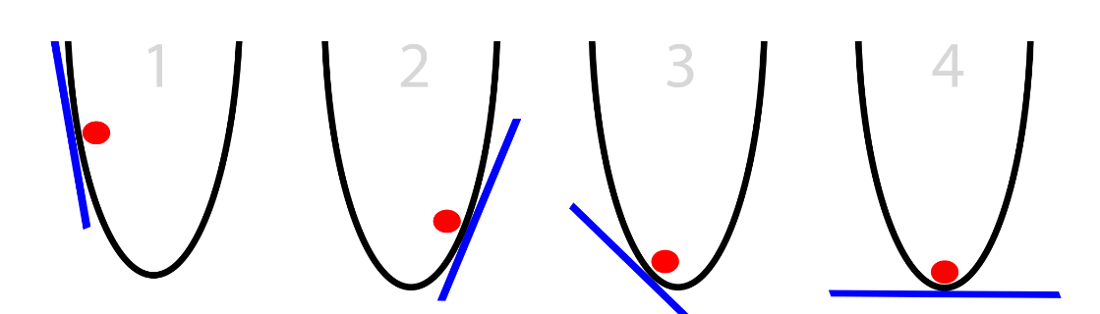
어떤 정보를 사용해서 공의 위치를 조정?
- 현재 공이 있는 지점의 바구니 밖의 기울기가 얻을 수 있는 유일한 정보 (위의 그림에서 파란색 선에 해당)
- 만약 기울기가 음수라면, 왼쪽에서 오른쪽으로 기울여진 것 -> 공은 오른쪽으로 이동
- 기울기가 양수라면, 공은 왼쪽으로 이동
-> 이러한 반복을 통해서 바구니의 바닥 지점을 찾음
(>> 최적화의 부분으로 Gradient Optimization이라고 함)
- 편미분 개념 사용 (-> 여기서 연속 함수인 시그모이드 함수를 활성화 함수로 사용)
🧐 EBP 학습 규칙
(사용하는 활성화 함수 = 시그모이드 함수)
- 가중치와 임계치를 초기화
- 입력과 목표 출력을 제시
- 제시된 입력 벡터를 이용해서 은닉층 j번째 뉴런으로 입력값 계산
- 시그모이드 함수를 사용해 은닉층의 출력을 계산
- 은닉층의 출력을 이용해서 출력층 뉴런 k로의 입력값을 계산
- 시그모이드 함수를 사용하여 출력층의 출력을 계산
- 입력 패턴의 목표 출력과 실제 출력과의 오차값을 계산하고 출력층 오차합을 학습 패턴의 오차로 누적
- 출력층 오차값과 은닉층과 출력층의 가중치 값을 이용하여 은닉층의 오차를 계산
- 4단계와 7단계를 통해 구한 은닉층 뉴런 j의 출력값과 출력층의 오차 값을 사용하여 출력치의 가중치를 갱신
- 출력층과 마찬가지로 입력층과 은닉층의 가중치 값을 갱신
- 모든 학습 패턴에 대하여 전부 학습할 때까지 2단계로 분기하여 반복 수행
- 출력층의 오차합 E가 허용값 이하이거나 최대 반복 회수보다 크면 종류, 그렇지 않으면 2단계로 가서 반복
Multi Layer Perceptron 정리
- 오류 역전파 개념 사용
- 은닉층의 학습을 위해 출력층에서 발생한 오류를 이용하여 은닉층의 오차를 계산
- 다시 이 값을 입력층으로 역전파시켜 출력층의 오차가 원하는 수준이 될 때까지 반복
- 실제 적용시 고려사항
- 최소평균제곱 비용함수의 국부 최적해를 위해 뉴런 수를 증가
- 이득항을 낮춰야 함
- 초기 가중치를 다르게 하여 여러 번 학습
- 문제점
- 상위층의 목표값과 실제 출력값 간의 오류를 하위층으로 역전파 시키는 것은 타당하지 않음 (-> 목표를 알지 못함)
- 오류 수렴까지 많은 회수의 학습을 반복하게 됨
- 지도학습에서 사용
'Daily > SWU' 카테고리의 다른 글
| 인공지능 - Neural Network (0) | 2022.04.17 |
|---|---|
| 알고리즘 - 패턴인식 (0) | 2022.04.17 |
| 인공지능 - 개요 (0) | 2022.04.17 |