#노드 클래스 생성
class Node<T: Comparable> {
var data: T
var left: Node?
var right: Node?
init(data: T) {
self.data = data
}
}
이진 탐색 트리의 경우 몇가지 조건이 있다.
✅ 데이터를 비교하면서 탐색을 하기 때문에 비교 가능한 데이터만 저장할 수 있도록 Comparable 프로토콜을 채택한 제너릭으로 선언했다.
✅ 데이터는 항상 존재해야 하므로 Non-Optional Type이다.✅ (데이터는 옵셔널이 아니지만) 트리의 왼쪽, 오른쪽 자식 노드는 있을 수도 있고 없을 수도 있기 때문에 Optional Type이다.
#이진 탐색 트리 클래스 생성
위에서 생성한 노드 클래스를 바탕으로 이진 탐색 트리를 구현해보자.
먼저, 최상위 노드인 root 노드를 만들면 아래와 같다.
class BinarySearchTree<T: Comparable> {
var root: Node<T>?
}
그리고 최상위 노드로부터 데이터를 삽입해서 구조를 만들어보자.
insert
func insert(_ data: T) {
// 만약 루트 노드가 존재하지 않는다면, 전달 받은 데이터로 노드를 생성해서 루트 노드로 만든다.
guard let root = self.root else {
return self.root = Node.init(data: data)
}
// 부모 루트를 현재 노드로 지정하고
var currentNode = root
while true {
// 현재 노드(= 탐색하는 노드)보다 값이 작다면
if currentNode.data > data {
// 계속 왼쪽으로 탐색하다가
guard let nextNode = currentNode {
// 만약 값이 nil이라면, 노드를 생성해서 삽입
return currentNode.left = Node.init(data: data)
}
// 값이 존재하면 계속 탐색
currentNode = nextNode
} else { // 노드보다 값이 큰 경우는 오른쪽으로 탐색
guard let nextNode = currentNode.right else {
return currentNode.right = Node.init(data: data)
}
currentNode = nextNode
}
}
}
let BST = BinarySearchTree<Int>()
BST.insert(20)
BST.insert(15)
BST.insert(30)
BST.insert(11)
BST.insert(17)
BST.insert(36)
BST.insert(38)
BST.drawDiagram()값을 넣고 그려보면 아래와 같이 나타난다.

search
찾는 데이터가 이진 탐색 트리 안에 존재하는지, 아닌지 판별해서 Bool 형으로 반환하는 함수를 만들어보자.
위의 삽입과 비슷하게 값을 비교하면서 찾는 값이 노드의 값보다 크면 계속 오른쪽 자식 노드로 이동해서 값을 찾는 것이고
노드의 값보다 작으면 계속 왼쪽 자식 노드로 이동해서 값을 찾는 것이다.
값이 있다면 true를 반환하고,
그렇게 찾았지만 단말노드까지 왔다면 (자식 노드가 존재하지 않는다면) false를 반환한다.
func search(from data: T) -> Bool {
if root == nil { return false }
var currentNode = root
while let node = currentNode {
// 찾는 값에 해당하는 노드의 데이터가 있다면 true를 반환
if node.data == data {
return true
}
// 노드의 값보다 찾는 값이 작다면 왼쪽으로 이동
if node.data > data {
currentNode = node.left
}
// 노드의 값보다 찾는 값이 크다면 오른쪽으로 이동
else {
currentNode = node.right
}
}
// 단말 노드까지 이동했음에도 없다면 false 반환
return false
}
그리고 테스트를 해보면 아래와 같이 콘솔에 나타나는 것을 볼 수 있다.
print(BST.search(from: 20))
print(BST.search(from: 15))
print(BST.search(from: 27))
print(BST.search(from: 37))
remove
삭제하는 것은 삽입/탐색과 다르게 고려해야 하는 상황이 꽤 있다 ..
단순히 삭제하는 것이 아니라, 삭제한 뒤에 해당 노드를 기준으로 위/아래를 다시 연결해야 하기 때문이다.
크게 세가지 상황으로 나눠서 볼 수 있다.
① 자식 노드가 0개인 노드 삭제 (단말 노드 삭제)
단말 노드? 자식 노드가 없는 노드를 말한다.
이러한 단말 노드를 삭제하는 경우는 연결만 해제하면 된다. (= branch만 끊어주면 된다.)
크게 두가지 단계를 거치게 되는데
✔️ 삭제할 노드를 탐색하는 작업
✔️ 삭제할 노드의 부모 노드의 branch(left가 될 수도 있고, right가 될 수도 있다.)를 nil로 할당해서 연결을 끊어야 한다.
코드로 보면 아래와 같다.
func remove(from data: T) -> Bool {
// 0. 삭제할 노드, 삭제할 노드의 부모 노드 탐색
guard let root = self.root else { return false }
var parentNode = root
var currentNode: Node? = root
// 삭제할 노드 탐색
while let node = currentNode {
if node.data == data { break }
if node.data > data {
currentNode = node.left
} else {
currentNode = node.right
}
// 삭제할 노드의 부모 노드
parentNode = node
}
// 삭제할 노드
guard let deleteNode = currentNode else {
// 삭제할 노드 탐색 실패 (삭제할 값이 없는 경우)
return false
}
// 1. 단말 노드 삭제(Leaf Node)
if deleteNode.left == nil && deleteNode.right == nil {
// 삭제하는 노드의 값이 그 노드의 부모 노드의 데이터보다 작다면 왼쪽에 위치하므로 왼쪽 bracnh에 nil을 할당
if parentNode.data > data {
parentNode.left = nil
}
// 삭제하는 노드의 값이 그 노드의 부모 노드의 데이터보다 크다면 오른쪽에 위치하므로 오른쪽 bracnh에 nil을 할당
else {
parentNode.right = nil
}
return true
}
return false
}
테스트를 해보면
let BST = BinarySearchTree<Int>()
BST.insert(20)
BST.insert(15)
BST.insert(30)
BST.insert(11)
BST.insert(17)
BST.insert(36)
BST.insert(38)
BST.drawDiagram()
BST.remove(from: 38)
BST.drawDiagram()
38 이라는 데이터가 들어있는 노드(= 단말 노드)가 삭제된 것을 볼 수 있다.
② 자식 노드가 1개인 노드 삭제
삭제할 값을 가진 노드를 찾아서 삭제를 한 다음,
해당 노드의 부모 노드와 자식 노드를 연결하면 된다.
삭제할 노드의 부모 노드가 삭제할 노드의 자식 노드를 가리키게 하는 것이다.
코드로 구현하면 아래와 같다.
// 2. 자식이 1개 있는 노드 삭제
// 삭제할 노드의 왼쪽 자식 노드가 존재할 경우
if (deleteNode.left != nil) && (deleteNode.right == nil) {
if parentNode.data > data {
parentNode.left = deleteNode.left
} else {
parentNode.right = deleteNode.left
}
return true
}
// 삭제할 노드의 오른쪽 자식 노드가 존재할 경우
if (deleteNode.left == nil) && (deleteNode.right != nil) {
if parentNode.data > data {
parentNode.left = deleteNode.right
} else {
parentNode.right = deleteNode.right
}
return true
}
테스트를 하면 기존의 구조에서 30을 삭제하는 경우가 자식 노드가 1개인 노드를 삭제하는 경우이다.

이렇게 30을 삭제하고 30을 기준으로 부모 노드인 20과 30의 자식 노드인 36이 서로 연결된 것을 볼 수 있다.
③ 자식 노드가 2개인 노드 삭제
자식 노드가 2개 있는 노드는 생각할 것이 좀 더 .. 있다 ..

예를 들어서 위와 같은 이진 탐색 트리가 있을 때, 자식 노드가 2개인 노드는
(루트 노드를 제외하고) 20, 32, 25이다.
만약 이중에서 20을 삭제하고 싶다고 할 때 이 때의 경우의 수는 2개가 있다.
- 20을 삭제하고 싶다.
- 20의 오른쪽 자식 노드 중, 가장 작은 값을 찾아(= 23) 20의 부모인 40과 연결한다.
- 20의 왼쪽 자식 노드 중, 가장 큰 값을 찾아(= 12) 20의 부모 노드인 40과 연결한다.
이진 탐색 트리는 삽입부터 정렬이 되어 있는 구조이므로
✅ 오른쪽 자식 노드의 가장 작은 값은, 오른쪽 자식 노드 중 가장 왼쪽에 위치한 단말 노드를 의미한다.
✅ (같은 맥락으로) 왼쪽 자식 노드의 가장 큰 값은, 왼쪽 자식 노드 중 가장 오른쪽에 위치한 단말 노드를 의미한다.
이 두가지 경우 중 하나를 선택해서 20을 삭제하고 다음 작업을 진행하면 된다.

위와 같은 이진 탐색 구조에서 1번 방법을 통해서 삭제 > 연결하면

이렇게 결과가 나타나고
2번 방법을 통해서 삭제 > 연결하면

이렇게 결과가 나타난다.
#이진 탐색 트리의 장점
탐색 속도가 빠르다.
그래서 데이터를 탐색할 때 자주 사용한다.
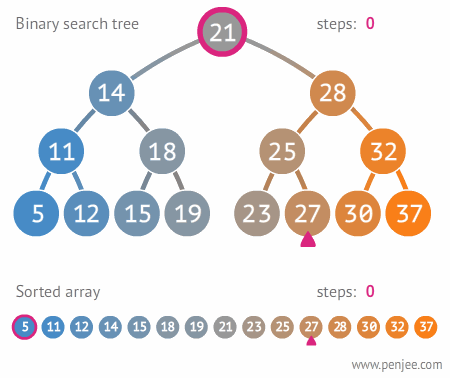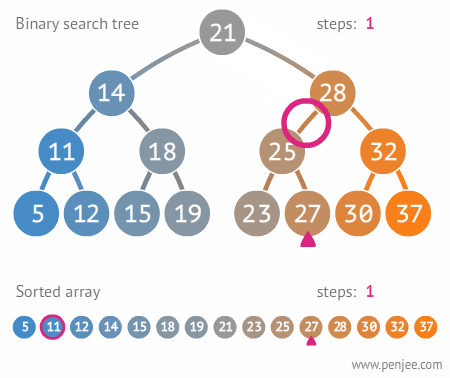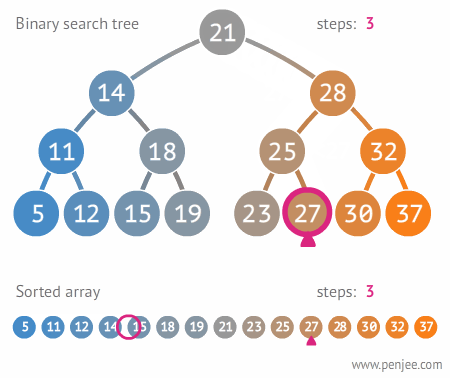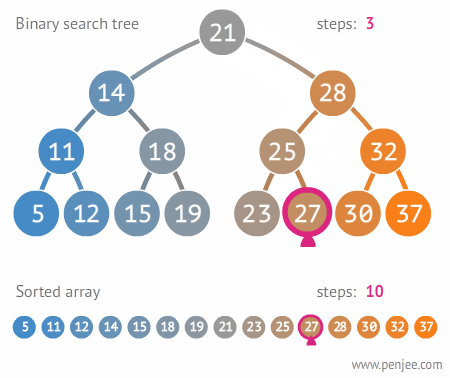
위 이미지를 통해서 배열과의 탐색 속도 차이를 볼 수 있다.
배열이 11번 탐색할 동안, 이진 탐색 트리는 3번 탐색한다.
그런데 만약
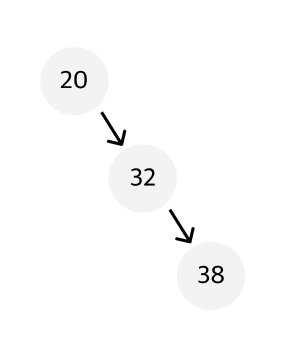
이렇게 한쪽 방향으로만 자식 노드가 존재하는 이진 탐색 트리의 경우 배열과 탐색 속도가 다르지 않다.
이 때의 시간 복잡도는 O(n)으로 배열과 동일하다.
따라서 이런 경우를 제외하면 이진 탐색 트리의 시간 복잡도는 O(logn)으로 훨씬 빠르다는 것을 알 수 있다.
참고 자료 :
https://babbab2.tistory.com/91?category=908011
Swift) 이진 탐색 트리(BST) 구현 해보기 (2/2)
안녕하세요 :) 소들입니다!!! 오늘은 저번 포스팅에 이어 이진탐색트리에 대해 끝맺음을 해보려고 해요!!! 저번에 insert, search 하는 방법을 봤었다면, 이번 포스팅에선 노드를 remove하는 방법에 대
babbab2.tistory.com
'Data Structure' 카테고리의 다른 글
| [자료구조] Deque (0) | 2022.10.17 |
|---|---|
| [자료구조] 트리, 이진트리, 이진탐색트리 (개념) (1) | 2022.10.13 |
| [자료구조] 그래프 (0) | 2022.09.28 |
| [자료구조] Queue (0) | 2022.09.27 |
| [자료구조] Stack (0) | 2022.09.26 |